Este texto é sobre normalidade, normalidade estatística e normatividade. Vem a propósito do dia internacional da mulher e das acusações de radicalismo que tendo a sofrer nesta altura por defender a igualdade. Tentarei argumentar que conceitos simples de estatística são úteis para compreender que a normatividade não é “natural”.
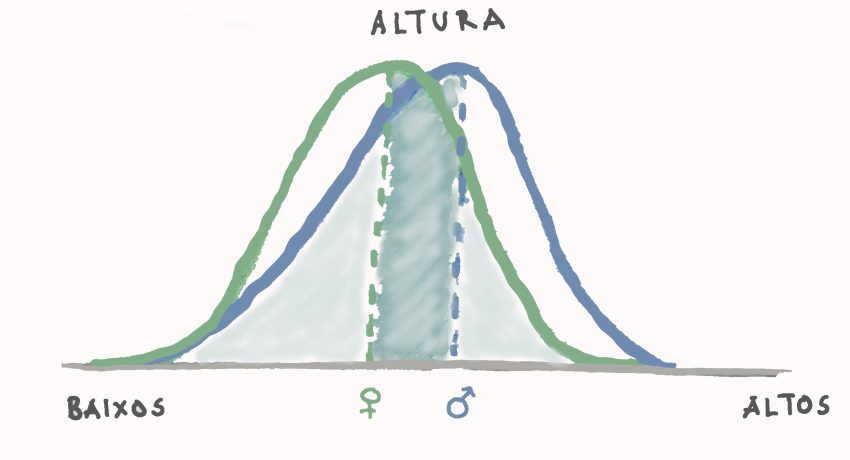
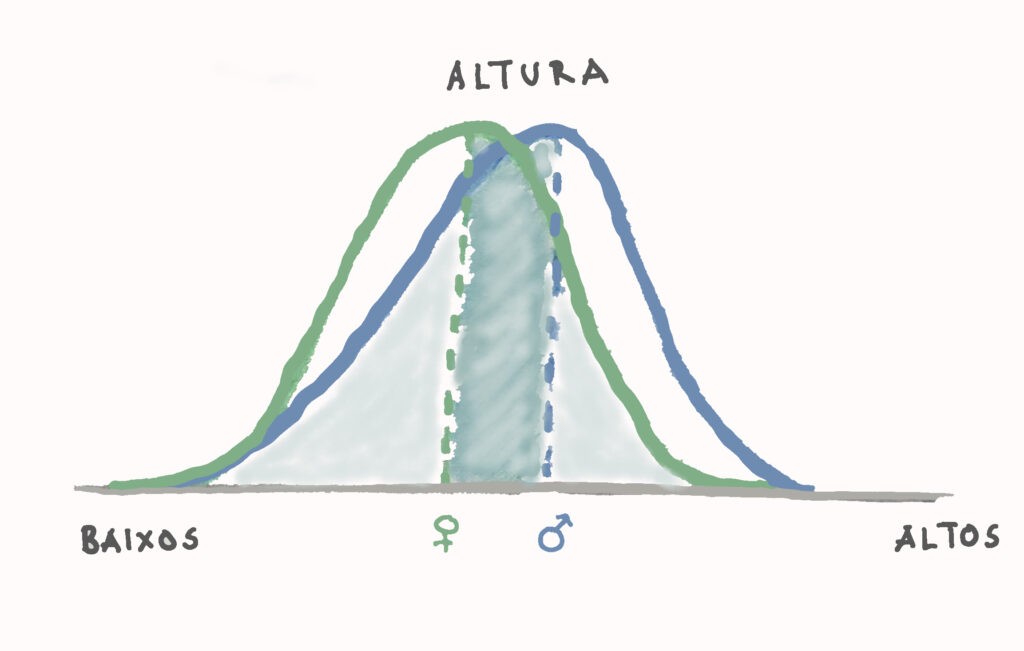
No dia 15 de Julho de 1940, aos 22 anos de idade, morria nos EUA Robert Wadlow, o homem mais alto do mundo. Por causa de uma doença hormonal, à data da sua morte media 2,72 m e pesava quase 200 kg. Segundo a Wikipedia, Wadlow foi, até hoje, o único humano a ultrapassar a barreira dos 2,7 m sendo que há registo de apenas 6 pessoas terem medido mais do que 2,6 m, todas elas homens. Do outro lado do espectro: a pessoa mais pequena de que há registo verificado foi o nepalês Chandra Bahadur Dangi, que morreu em 2015 com 54,64 cm. Na lista das pessoas mais baixas encontramos apenas 7 com 65 cm ou menos, sendo que 3 destas são mulheres. A altura depende de uma série de factores (genéticos, sociais) e para se ser muito alto ou muito baixo é preciso que vários se conjuguem: é uma questão de sorte, ou de azar. Mas é geralmente aceite que os homens são mais altos do que as mulheres, e que as pessoas de países ricos do hemisfério norte (p. ex. Dinamarca, altura média dos homens 180,4 cm) tendem a ser mais altas do que as pessoas de países pobres do hemisfério sul (p. ex. Timor-Leste, altura média das mulheres 152,9 cm). No entanto, escolhendo uma pessoa ao acaso e sabendo apenas a sua altura não é possível determinar com certeza o seu sexo ou a sua nacionalidade.
Uma forma de visualizar isto é desenhar a distribuição de probabilidades das alturas: se pegarmos em todos os humanos e os ordenarmos, irá aparecer uma curva muito simples, a que chamamos curva Normal, Gaussiana, ou em forma de sino. Vemos que há muito poucas pessoas extremamente altas e muito poucas extremamente baixas, mas muitas de uma altura “normal”, ou seja, no meio do sino (como na figura mal desenhada). Em média, os homens são mais altos do que as mulheres, mas as duas curvas têm muita sobreposição: temos mais homens nos dois extremos da curva e escolhendo um ponto à sorte no gráfico não temos forma de saber a que curva pertence, ou seja, se eu disser a altura de alguém, a não ser que essa pessoa tenha uma altura muito extrema, não há como adivinhar se corresponde a um homem ou a uma mulher.
Esta curva foi desenhada pela primeira vez por Abraham de Moivre, no século XVIII, quando estava a tentar ajudar jogadores a vencer no “cara ou coroa” (jogar jogos de azar, como lançar moedas, dados ou poker torna as pessoas bastante boas em estatística). Agora sabemos que esta distribuição surge sempre que os acontecimentos não dependem uns dos outros (sair uma vez “cara” não implica que saia “cara” outra vez) e que eles tenham a mesma probabilidade de acontecer (desde que a moeda não esteja viciada). Então, estatisticamente, a ideia de normalidade quer dizer seguir uma distribuição Normal, ou seja, desenhar uma curva destas. É uma distribuição muito comum e também surge supostamente se compararmos testes de QI (poucas pessoas com QI muito alto ou muito baixo) e poderia surgir nos rendimentos (muito poucos muito ricos ou muito pobres, uma classe média maior, o que nem sempre é verdade porque muitas vezes “a moeda está viciada”).
Quando se discute “normalidade” fora do contexto matemático, por vezes acontece algo interessante: a normalidade deixa de ser vista como a curva toda ou até como o valor médio da curva (“normalmente” o ponto em que a curva é mais alta, ou o centro do sino), mas como o seu extremo. Por exemplo, imaginemos que desenho a curva de probabilidades de crianças do sexo masculino gostarem de brincar com carrinhos.Haverá os que gostam muito e os que gostam pouco e uma maioria que gosta “mais ou menos”. Se fizer esta curva para crianças do sexo feminino é possível que esta esteja deslocada para a esquerda e não é fácil saber se é porque de facto gostam menos ou apenas porque a sociedade decidiu que carrinhos não são uma boa prenda para dar a meninas. Mas, a não ser que os meninos sejam obrigados a fazê-lo e as meninas sejam proibidas de o fazer (e, nesse caso, a moeda está viciada), será altamente improvável que não exista qualquer sobreposição entre as curvas, ou seja, é improvável que todos os meninos gostem imenso de brincar com carrinhos e que nenhuma menina goste de o fazer. Então, havendo bastante sobreposição entre as curvas e meninos que não gostam nada e meninas que gostam mesmo muito, saber que uma criança gosta de brincar muito com carrinhos não é suficiente para eu lhe conseguir adivinhar o sexo. Para complicar as coisas, posso fazer o mesmo gráfico com muitas outras preferências e comportamentos (como preferência por determinadas cores), identificar diferenças ligeiras e, mesmo sem entrar na discussão sobre estas diferenças serem inatas ou socialmente impostas, perceber que quase nunca é possível separar completamente as curvas. Por isso, a não ser que todas estas preferências estejam ligadas e que gostar de azul aumente a probabilidade de gostar de futebol (argumento que alguns benfiquistas talvez disputem), a probabilidade “natural” de todas as meninas serem pouco assertivas, só gostarem de brincar com bonecas cor-de-rosa e com unicórnios e de todos os meninos terem muita energia e só gostarem de carros azuis e de espadas começa a aproximar-se da probabilidade de terem 2,70 m. Isto implica que, independentemente de acharmos ou não que existem diferenças inatas entre sexos, é muito improvável que tantas crianças encaixem tão “naturalmente” em padrões tão específicos. Pelo contrário, sugere que tanta normatividade é imposta socialmente: estamos a viciar as moedas.
Mas que mal poderá advir de viciar as moedas, se isto ajuda as nossas crianças e a sociedade? Suponho que talvez ajude indivíduos com capacidade de se adaptarem ao contexto presente mas, certamente, não ajuda muitos outros que se sentem deslocados e cuja “normalidade” é vista como antinatural. Mas penso que o impacto negativo desta pressão normativa se revela de forma mais óbvia ao nível da população: algo que a biologia nos ensina é a importância da diversidade, por ser na diversidade que a selecção natural actua, permitindo encontrar soluções quando o ambiente muda. Se continuarmos a sustentar esta normatividade não-natural, corremos o risco de eliminar da população diversidade inata e com isso, eliminar futuros Einsteins, Curies, Regos ou Warhols.